Structure-driven optimization methods for modular technical systems¶

The term structure-driven refers to the following idea. First, we partition the large, sparse nonlinear model of a technical system into smaller subproblems. Then, a suitable ordering of these smaller problems is determined so that the solution to the original problem can be reconstructed from the solutions of the smaller ones. The decomposition just sketched resembles the tree decomposition, which is very popular in discrete optimization and constraint satisfaction; this project deals with continuous problems. Evidence shows that appropriate decomposition can speed up the computations by several orders of magnitude.
Nonlinear programming is meant by optimization.
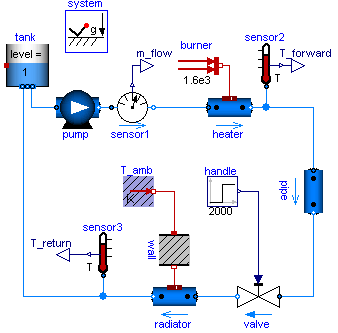
The image below shows an example of a modular technical system (a heating system, the image has been taken from the Modelica website). Component-based modeling is well suited for modular technical systems; Simulink and Dymola are examples of component-based modeling tools. The modules (components) of the technical systems help in decomposing the large model into smaller problems.

The source code is available on GitHub under the 3-clause BSD license.

THIS PROJECT IS A WORK IN PROGRESS.

Input¶

Currently, the models are written in AMPL, and after some black magic, the expressions are built-up in memory as a direct acyclic graph (DAG), using NetworkX DiGraph. It is somewhat similar to the expression trees in SymPy. Only nonlinear systems of equations are considered at the moment (steady-state modeling).

For example, the following AMPL code

var x; var y; var z;
equation: exp(3*x+2*y)+4*z = 1;

yields the directed acyclic graph below.

In the future, I would like to use either Python or JuMP for building the models. In any case, I will keep the AMPL interface too. Modelica is definitely on the agenda, accessed through the functional mock-up interface. This project is not aiming at creating yet another modeling environment: The goal is to plug the tools of this project into well-established modeling systems.

Reverse mode automatic differentiation¶

Source code is generated from the DAG representation of the expressions in order to compute the Jacobian with reverse mode automatic differentiation. Currently only Python code is emitted, in the near future, templated C++ code will also be generated. For example, for the above example exp(3*x+2*y)+4*z the following Python code is generated (hand-edited to improve readability):

# f = exp(3*x+2*y)+z
# Forward sweep
t1 = 3.0*x + 2.0*y
t2 = exp(t1)
f = 4.0*z + t2 - 1.0
# Backward sweep
u0 = 1.0
u1 = 4.0 * u0  # df/dz = 4
u2 = u0
u3 = t2 * u2
u4 = 3.0 * u3  # df/dx = 3*exp(3*x+2*y)
u5 = 2.0 * u3  # df/dy = 2*exp(3*x+2*y)

The templated C++ version of this code will greatly benefit from code optimization performed by the C++ compiler; I expect the generated code to be as good as hand-written.

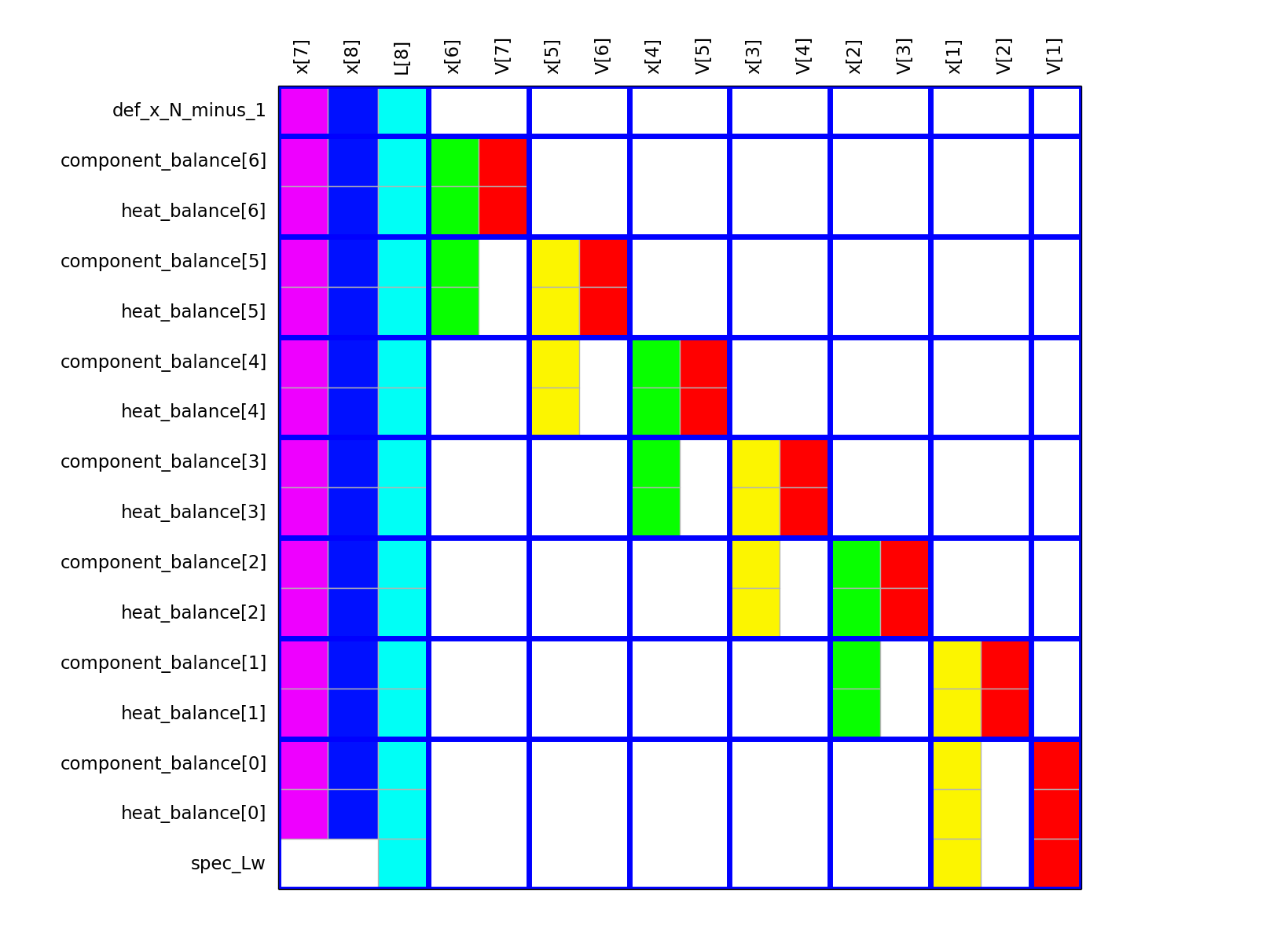
Natural block structure¶

The modules of the technical systems partition the Jacobian into blocks in a fairly natural way. This natural block structure plays an important role in structure-driven algorithms: Computing the optimal partitioning and ordering of the smaller subproblems is NP-hard in the general case; one must resort to heuristics in practice. Independent results show that the heuristic which exploits the natural block structure often yields good quality partitioning and ordering.

The current way to pass the natural blocks is rather hackish: Suffixes are used, see Defining and using suffixes on page 302 in the AMPL book. In the future, component-based modeling tools will hopefully allow programmatic access to the natural block structure.

Minimum degree ordering¶

A basic minimum degree ordering has been implemented. The blue lines show the natural block structure.

My primary interest is chemical process modeling. The Jacobian of these models are very sparse but highly unsymmetric, numerically indefinite, not diagonally dominant and possibly ill-conditioned. There are many packages for the symmetric and slightly unsymmetric case. (In the slightly unsymmetric case, it is acceptable to introduce artificial fill-in to make the sparsity pattern symmetric and then use a sparse matrix ordering algorithm, developed for the symmetric case.) I have only found MC33 from the Harwell Subroutine Library that is applicable in the highly unsymmetric case. Since MC33 is based on a heuristic, it unfortunately fails on those chemical process models that are of interest to me.

Graph coloring¶

Depending on the implementation, efficient forward-mode automatic differentiation may require well-chosen seed vectors; these seeds can be computed with graph coloring. Even though graph coloring is NP-complete in general, the minimum degree ordering enables an efficient greedy coloring heuristic.